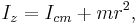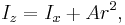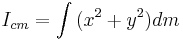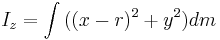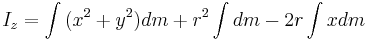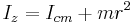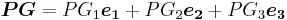Parallel axis theorem

In physics, the parallel axis theorem or Huygens-Steiner theorem can be used to determine the second moment of area or the mass moment of inertia of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's centre of mass and the perpendicular distance (r) between the axes.

The moment of inertia about the new axis z is given by:

$I_z = I_{cm} %2B mr^2,\,$

where:

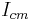$I_{cm}\!$ is the moment of inertia of the object about an axis passing through its centre of mass;

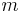$m\!$ is the object's mass;

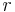$r\!$ is the perpendicular distance between the two axes.

This rule can be applied with the stretch rule and perpendicular axis theorem to find moments of inertia for a variety of shapes.

The parallel axes rule also applies to the second moment of area (area moment of inertia) for a plane region D:

$I_z = I_x %2B Ar^2,\,$

where:

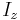$I_z\!$ is the area moment of inertia of D relative to the parallel axis;

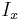$I_x\!$ is the area moment of inertia of D relative to its centroid;

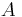$A\!$ is the area of the plane region D;

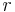$r\!$ is the distance from the new axis z to the centroid of the plane region D.

Note: The centroid of D coincides with the centre of gravity (CG) of a physical plate with the same shape that has uniform density.

1 Proof
2 In classical mechanics
3 See also
4 References

Proof

We may assume, without loss of generality, that in a Cartesian coordinate system the perpendicular distance between the axes lies along the x-axis and that the centre of mass lies at the origin. The moment of inertia relative to the z-axis, passing through the centre of mass, is:

$I_{cm} = \int{(x^2 %2B y^2)} dm$

The moment of inertia relative to the new axis, perpendicular distance r along the x-axis from the centre of mass, is:

$I_z = \int{((x - r)^2 %2B y^2)} dm$

If we expand the brackets, we get:

$I_z = \int{(x^2 %2B y^2)} dm %2B r^2 \int dm - 2r\int{x} dm$

The first term is I_cm, the second term becomes mr², and the final term is zero since the origin is at the centre of mass. So, this expression becomes:

$I_z = I_{cm} %2B mr^2\,$

In classical mechanics

In classical mechanics, the Parallel axis theorem (also known as Huygens-Steiner theorem) can be generalized to calculate the inertia tensor J_ij about a generic point P, given the inertia tensor I_ij about the centre of mass G:

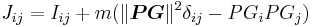
$J_{ij}=I_{ij} %2B m(\|\boldsymbol{PG}\|^2 \delta_{ij}-PG_iPG_j)\!$

where

$\boldsymbol{PG}=PG_1\boldsymbol{e_1}%2BPG_2\boldsymbol{e_2}%2BPG_3\boldsymbol{e_3}\!$

is the vector from point P to the centre of mass G, and 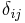$\delta_{ij}\!$ is the Kronecker delta.

We can see that, for diagonal elements (when i = j), displacements perpendicular to the axis of rotation results in the above simplified version of the parallel axis theorem.

References